线性优化问题是运筹学当中的一种发展较为成熟的问题，很多实际优化问题也都可建模或转化为线性优化问题。所以，了解如何通过线性优化求解器来解决线性优化问题就显得相当有必要了。

在本篇文章中，我们将始终使用同一个实例，从而能够更方便地在不同线性规划求解器之间进行对比。

待优化问题

资源 A B C 存量
煤炭 1 3 0 12
人力 3 2 3 13
仓库 3 3 5 20
收益 3 10 3 /

决策变量

变量名 含义
\(x_1\) 产品 A 生产量
\(x_2\) 产品 B 生产量
\(x_3\) 产品 C 生产量

目标函数

$$ \mathrm{max}~3 \cdot x_1 + 10 \cdot x_2 + 3 \cdot x_3 $$

约束条件

$$ x_1 + 3 \cdot x_2 \le 12 $$ $$ 3 \cdot x_1 + 2 \cdot x_2 + 3 \cdot x_3 \le 13 $$ $$ 3 \cdot x_1 + 3 \cdot x_2 + 5 \cdot x_3 \le 20 $$ $$ x_1, x_2, x_3 \ge 0 $$

优化求解器

Microsoft Excel

  1. 输入对应公式至表格中

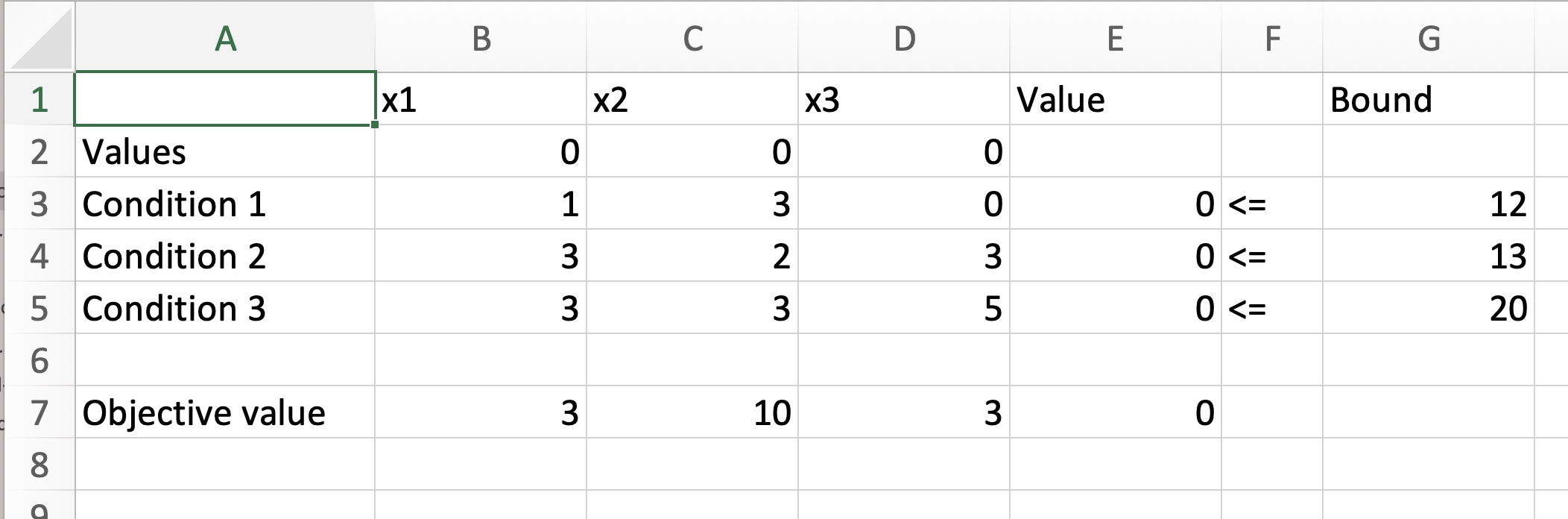
  2. 使用 Data -> Solver，打开求解器

  3. 输入对应要求

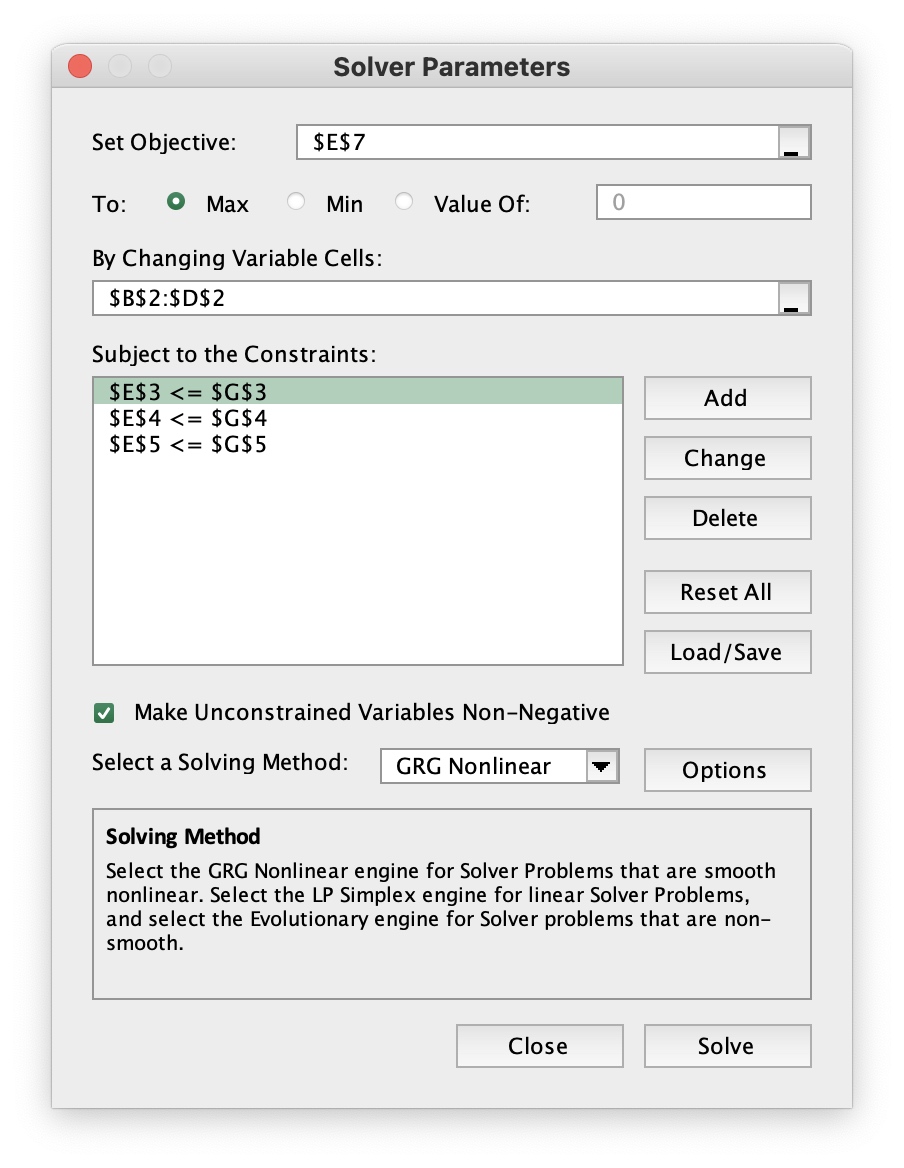
  4. 点击求解，获得求解结果

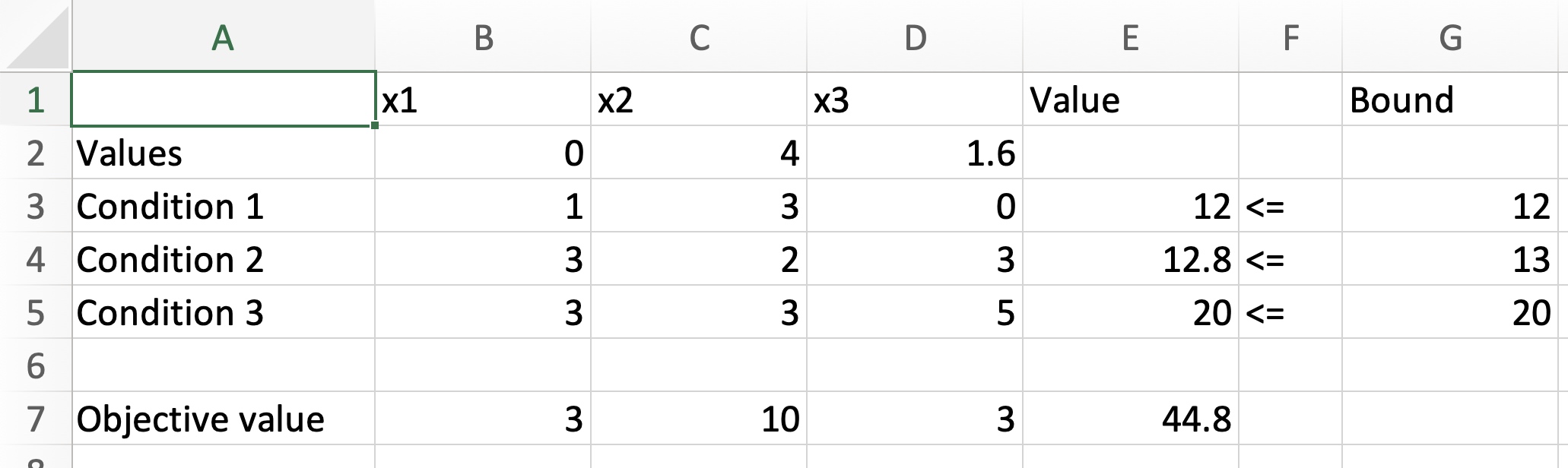
  5. 还可生成相关报告，以供参考

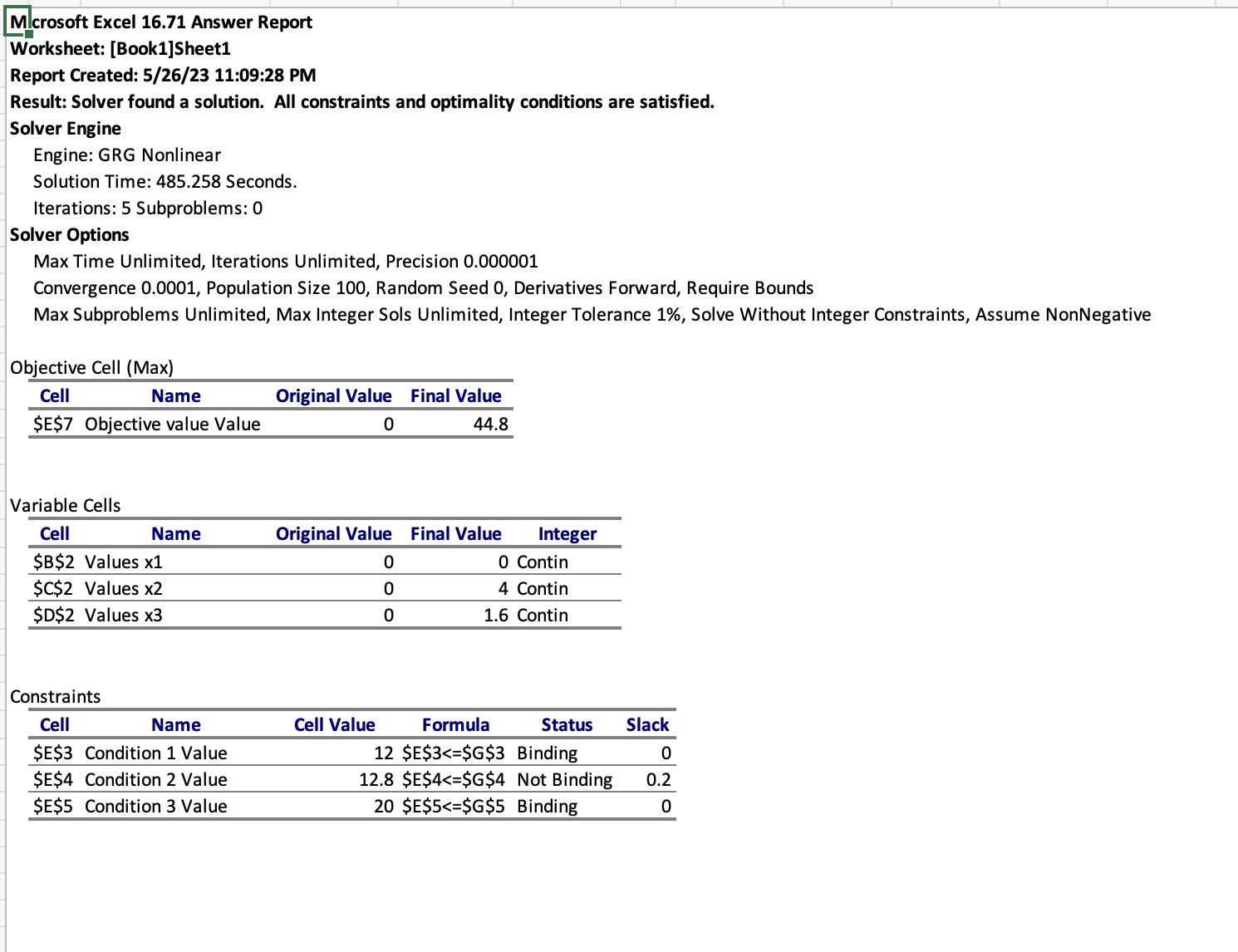
Lingo

  1. 输入对应模型
max 3x1 + 10x2 + 3x3
st
x1 + 3x2 <= 12
3x1 + 2x2 + 3x3 <= 13
3x1 + 3x2 + 5x3 <= 20

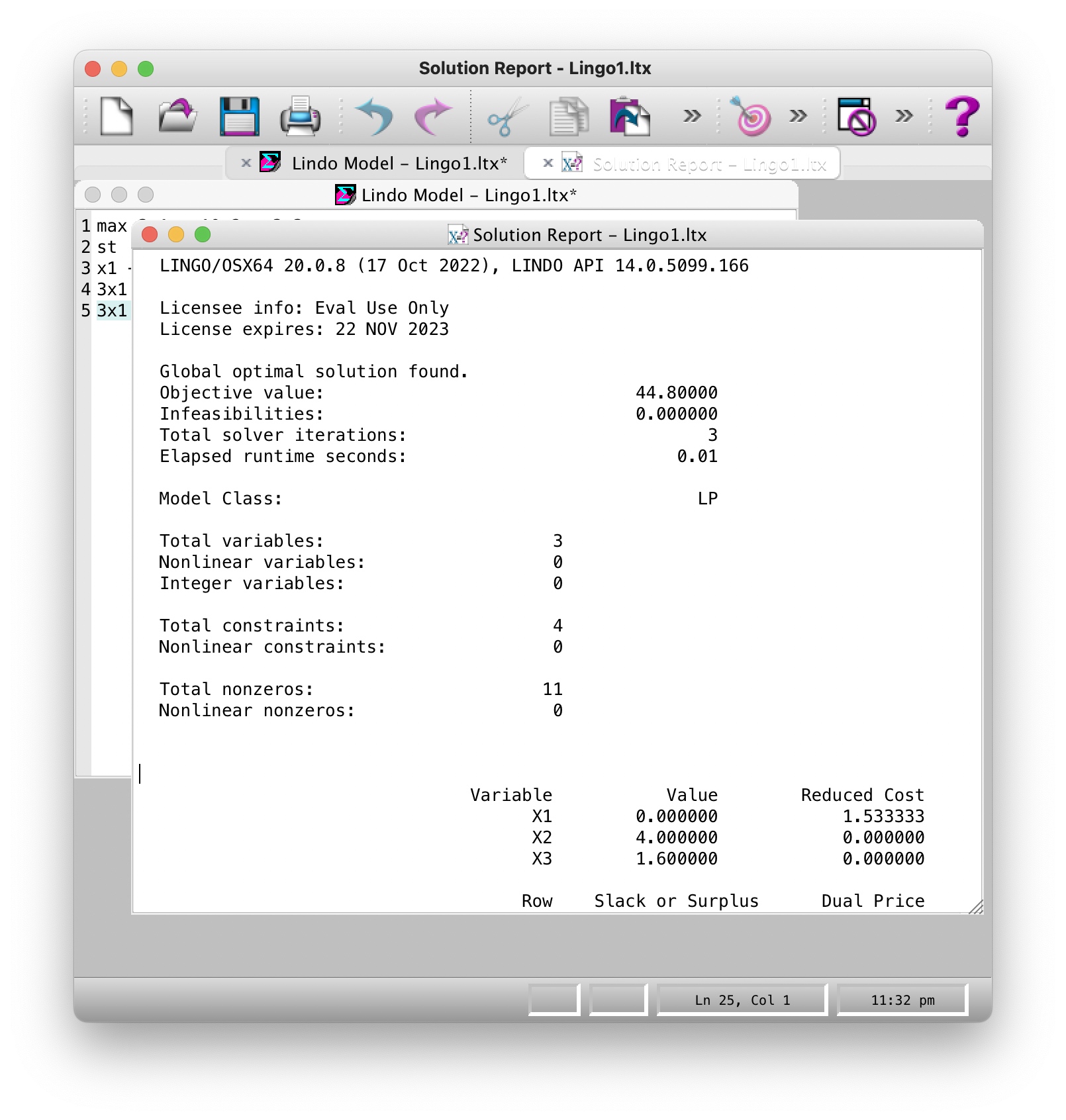
2. 点击求解，即可获得求解结果以及报告

Matlab

  1. 输入对应数值
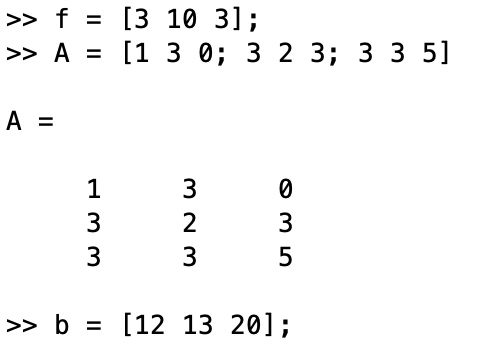
  2. 求解（注意，由于 Matlab 默认求解最小值问题，所以在本问题中需要在目标函数系数上都加一个负号）

Gurobi

（教育许可申请失败了，下次再试……）